The reciprocal of a real or complex number 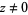is its multiplicative inverse 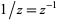, i.e., 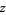to the power 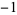. The reciprocal of zero is undefined. A plot of the reciprocal of a real number is plotted above for .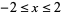

Two numbers are reciprocals if and only if their product is 1. To put it another way, a number and its reciprocal are inversely related. Therefore, the larger a (positive) number, the smaller its reciprocal.

The reciprocal of a complex number 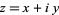is given by

Plots of the reciprocal in the complex plane are given above.

Given a geometric figure consisting of an assemblage of points, the polars with respect to an inversion circle constitute another figure. These figures are said to be reciprocal with respect to each other. Then there exists a duality principle which states that theorems for the original figure can be immediately applied to the reciprocal figure after suitable modification (Lachlan 1893).